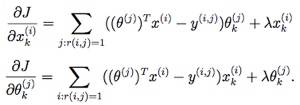超参数调整
training/dev/test集
dev集就是validation集,用于评估超参数选择的好坏。test集只在训练完成后做一次评估。要确保dev/test集的数据来自同一分布。如果来自实际应用的数据太少,优先划分到dev/test集。
bias和variance
high bias对应欠拟合,high variance对应过拟合
- 若training集误差比人类误差(比如0)高得多,说明high bias、欠拟合。
- 若dev集误差比training集误差高得多,说明high variance、过拟合。
- 若test集误差比dev集误差高得多,说明dev集过拟合,需要扩充dev集。
training集的数据可来自不同分布
如果training集的数据来自不同分布,就要从training集随机取些数据构成training-dev集。training-dev集与training集来自同一分布,但不参与训练,部分取代原先dev集的功能。
- 若training-dev集误差比training集误差高得多,说明high variance、过拟合。
- 若training-dev集误差和training集误差差不多,但dev集误差比training-dev集误差高得多,说明数据不匹配。这时要多制造或者采集符合dev/test集特征的training集数据。
防止过拟合
regularization(正则化):在代价函数J(w,b)中给权重矩阵w添加惩罚。一般用L2正则 \(||w||_2^2 = \sum w_j^2\),效果是参数值减小。 > L1正则 \(|w|_1 = \sum |w_j|\) 效果是参数值为0。因为|w|图像关于y轴对称,在x=0处取极小值。
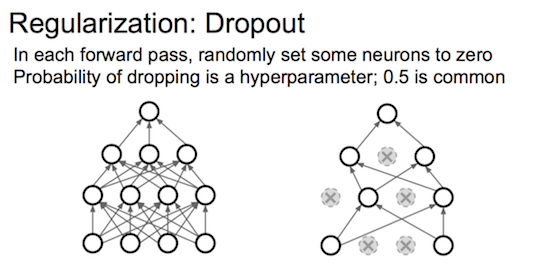
dropout(随机失活):每次前向-后向传播中,各层随机保留keep-prob比例的单元,并将单元输出/=keep-prob以弥补关掉单元的输出。各层的keep-prob参数可以不同。
data augmentation(数据扩展):比如把图片翻转、旋转、切变、裁切、变色等。
输入归一化(normalize)
\(x = (x-μ)/σ\),均值归0、方差归1
梯度爆炸或消失
梯度爆炸只需clipping掉太大的梯度。
梯度消失可从一些方面缓解,比如激活函数、权重矩阵初始化、跨层连接
- 将激活函数从tanh/sigmoid换成relu,因为relu当x>0时梯度为1,乘上不会减小。
- 将权重矩阵初始化为单位矩阵I。更常用Xavier初始化,使输入输出方差相同:\(rand()\sqrt{ \frac{1}{n_{in}} }\),\(n_{in}\)是该层输入单元的个数;若激活函数是relu,有一半情况不激活:\(rand()\sqrt{ \frac{2}{n_{in}} }\)。
- ResNet中跨层连接;RNN中使用GRU或LSTM等门单元。
mini-batch
每次只取m个样本,在这mini-batch上梯度下降。m大时算得快,因为mini-batch整体向量化参与计算。经验上最好m<=32,小mini-batch训练出的模型泛化能力更强。 特例:m=1,叫作stochastic梯度下降;m=总样本数,叫作batch梯度下降。
梯度下降的加速
高维空间容易遇到“鞍点”减慢下降速度,下面算法都能解决鞍点问题。
常用的Adam算法整合了Momentum和RMSprop
Momentum
指数加权移动平均:\(v_t = βv_{t-1} + (1-β)*θ_t\)。可修正初始偏差 \(v_t / (1-β^t)\)
用梯度的移动平均更新权重: \(V_{dW} = βV_{dW} + (1-β)dW\),\(W=W-αV_{dW}\)。b同理更新。
RMSprop(root mean square prop)
\(S_{dW}=βS_{dW} + (1-β)dW^2(dW^2按元素乘\)),\(W=W-α\frac{dW}{\sqrt{S_{dW}}}\)。 因为\(dW\)值较小,\(S_{dW}\)较小,\(\frac{dW}{\sqrt{S_{dW}}}\)较大,W移动变快,W方向收敛加快。
b同理更新,b移动变慢,b方向振荡减小。
学习率衰减(learning rate decay)
跑一遍数据叫1 epoch,随着epoch增加,减小学习率。
提前停止
一般不用这方法,因为它同时有两种不正交的影响:提高了dev集拟合、降低train集拟合。
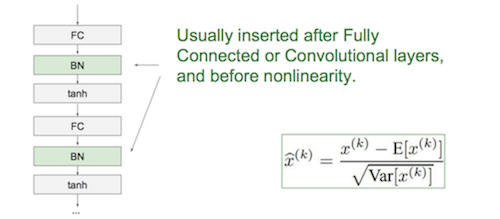
Batch Norm
隐藏层在应用激活函数a=g(z)前,先对该层z值进行归一化,使它们有相同的均值(不一定是0)和方差(不一定是1)。
新添BN层,输入z值计算均值μ和方差σ,\(z_{norm}^{(i)} = \frac{z^{(i)} - μ}{\sqrt{σ^2 + ε}}\),\(\tilde{z}^{(i)} = γz_{norm}^{(i)} + β\)。其中γ和β是待学习的参数,输出值\(\tilde{z}^{(i)}\)代替\(z^{(i)}\)进激活函数层。
使用BN时 \(z^{[l]} = W^{[l]}a^{[l-1]} + b^{[l]}\) 中的\(b^{[l]}\)项可省略,不省略也将被归一化减掉。
训练时在一个个mini-batch上应用BN,更新μ和σ的移动平均;测试时用μ和σ的移动平均作总体μ和σ的估算。
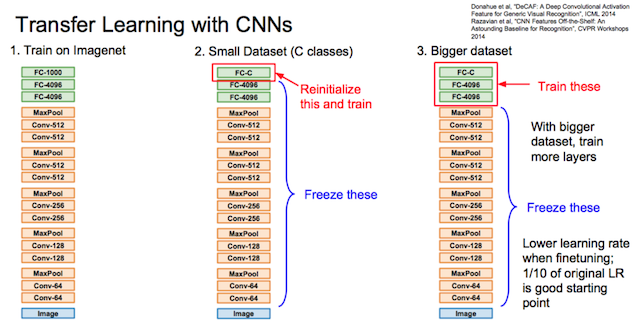
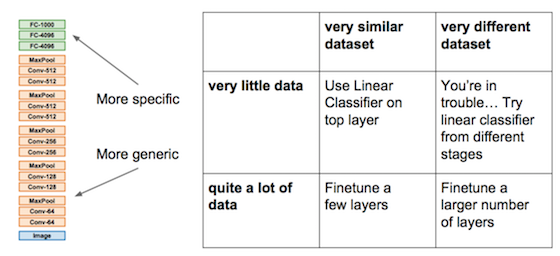
迁移学习
为利用大数据量任务A训练好的深度网络N,相同类型的小数据量任务B换掉N的最后几层换上新层,然后在最后一些层上更新权重(其余层不更新权重)。
如果更新所有层的权重,那么原先A上的训练叫做pre-training,现在B上的训练叫做fine-tuning。
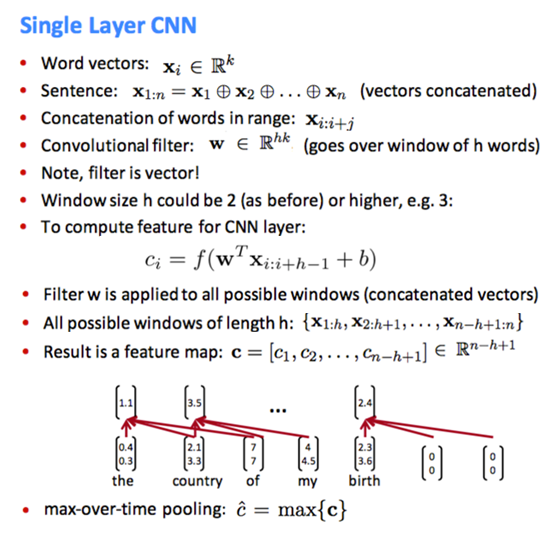
CNN
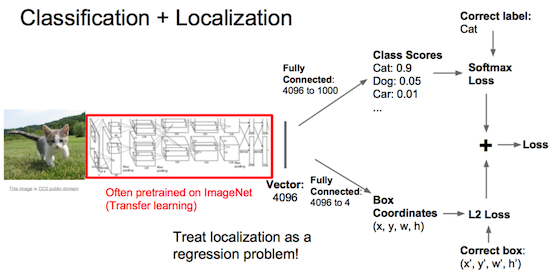
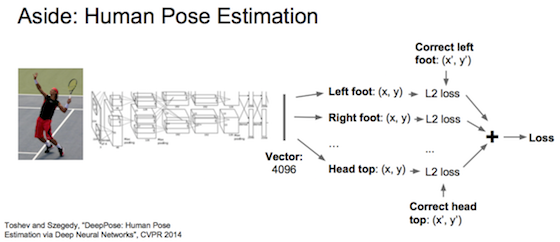
物体分类和定位一起做
图片中单物体定位:输出标签 anchorBox [ 图片是否包含物体?,若包含时物体定位框的四个点,物体的各个分类]。
滑动窗口算法:一小块一小块窗口卷积地看图片是否包含物体。 全卷积网络优化:把Convs-FullyConnected的网络改成Convs-1x1Convs的全卷积网络,然后在整个图片上卷积,一下子算出了各块窗口的卷积。
YOLO算法(You Only Look Once):把图片分成一些不重叠网格,每个网格对应输出中的一维anchorBox。物体中心在哪个网格则物体在哪个网格,每个网格识别中心落在该网格的物体。同样用全卷积网络,一下子算出各网格的卷积。
去掉多余定位框:两个矩形框的重叠率用IoU(Intersection over Union)表示。在物体定位时会找到大大小小多个定位框,首先去掉识别概率 < threshold的框;然后先选个概率最高的框k,去掉与k的重叠率较高的框(non-max supression,非极大值抑制),如此继续。
一个网格识别多个物体:各种形状矩形定义一个anchorBox,扩展输出标签 [anchorBox1, anchorBox2, anchorBox3…]
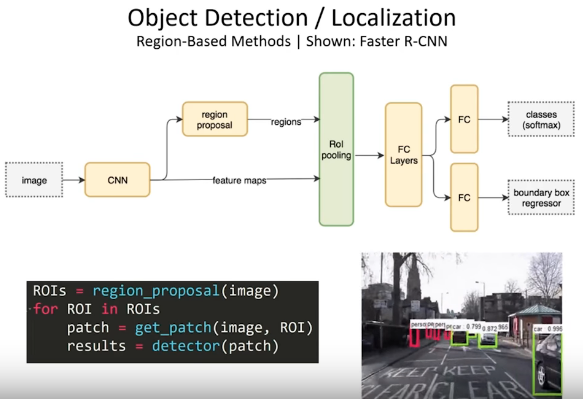
另:多物体的分类和定位,region-based CNN,先用分割算法找出些候选色块,再分类。
人脸识别:要训练相似度函数
Siamese网络是共享权值的两个相同网络Conv-Pool-FC,两个输出连到最后一层,训练的相似度函数。要使相同人脸的向量距离小、不同人脸的向量距离大。训练网络时是需要有同一人的多张人脸。 可以:每次同时输入三张图片,一张基准Anchor、一张相同人的Positive、一张不同人的Negative,要求\(d(A, P) + α <= d(A, N),α>0\)。\(L = max( d(A, P) - d(A, N) + α, 0 )\),α限制要显著地小。 或者:每次同时输入两张图片,最后做相不相似的二元分类。\(y = σ( \sum( w * | f^{(i)}_k - f^{(j)}_k | ) + b )\)
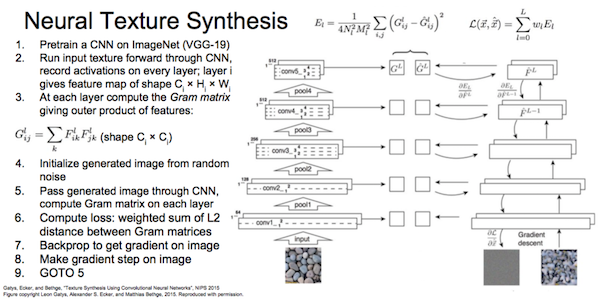
神经风格转换:给Content图片C加上Style图片S的风格
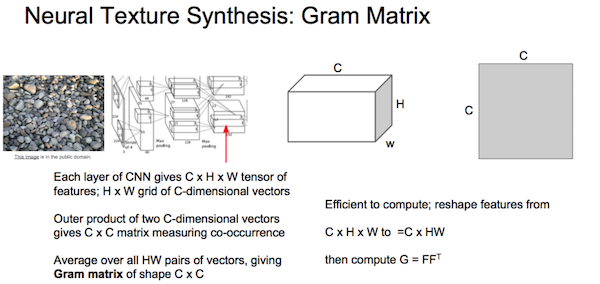
先随机生成图片G,然后最小化代价函数,根据梯度调整G。代价函数由内容和风格两部分构成,\(J(G) = αJ_{content}(C, G) + βJ_{style}(S, G)\)。 内容代价是在隐藏层L上计算与内容图片激活情况的差距,\(J_{content}(C,G) = 1/2 * || a^{C} - a^{G} ||_2^2\)。 风格是隐藏层L(w*h*c)的c个子层间的“相关性”。因为一个子层是一种卷积核运算的结果,表示提取了某种特性。两子层间的相关性表示两种特征同时出现的情况,各子层间的相关性表示各种特征同时出现的情况,就表示了某种风格。风格矩阵(Gram矩阵):维度c*c的矩阵,每个元素表示两个子层相同位置激活值相乘的的卷积值,是一种非标准的”相关性"。风格代价是在隐藏层L上计算和风格图片的Gram矩阵的差距,\(J_{style}(S, G) = 1/(2hwc)^2 || Gram^{S} - Gram^{G} ||_2^2\)。 最后,不仅考虑某隐藏层L,所有层都可以加入到损失函数计算中,这就考虑了各层风格。
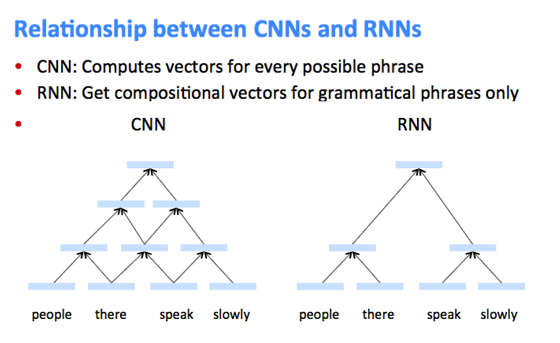
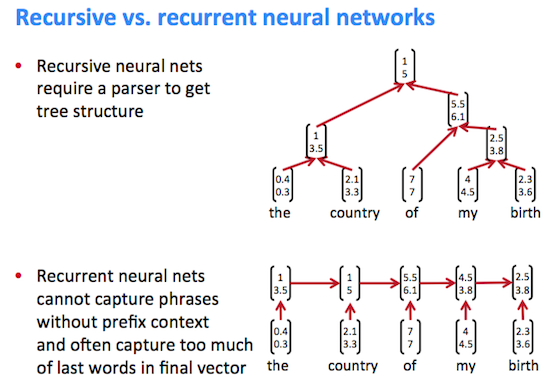
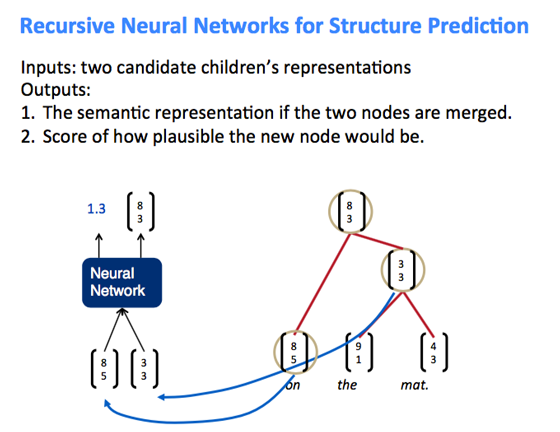
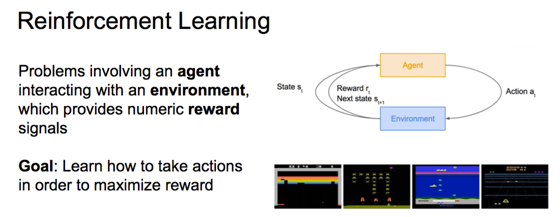
序列模型
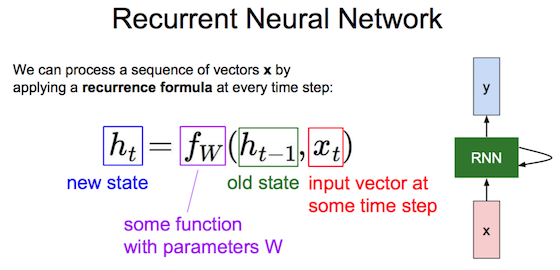
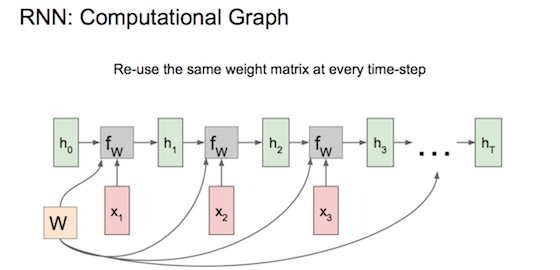
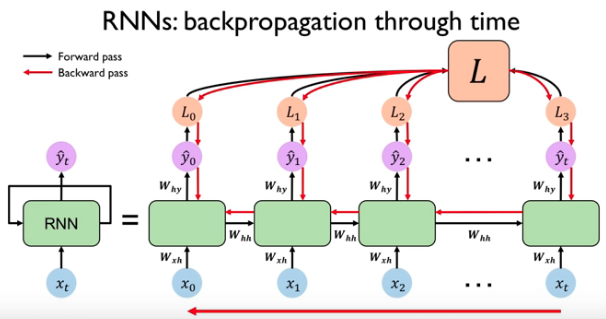
RNN(循环神经网络)
t时刻输入\(x_t\),t-1时刻激活值\(a_{<t-1>}\)参与当前激活值计算 \(a_{<t>} = g( w_{aa}a^{<t-1>} + w_{ax}x^{<t>} + b_{a} )\),当前预测值 \(y^{<t>} = g( w_{ya}a^{<t>} + b_{y} )\)。计算激活值时的g通常选tanh、偶尔relu,计算预测值时的g根据分类问题二元sigmod、多元softmax。 \([A,B]\)表示两矩阵横向拼接、\([A;B]\)表示两矩阵竖向拼接,让\(w_{a} = [w_{ax}, w{ax}]\),\(a_{<t>} = g( w_{a} [a^{<t-1>}; x^{<t>}] + b_{a} )\)
语言模型
有个词表,单词用词表长one-hot向量表示。每次输入一个单词,输出此刻各个单词的概率。最小化代价是各时刻猜测概率与实际出现单词的交叉熵。
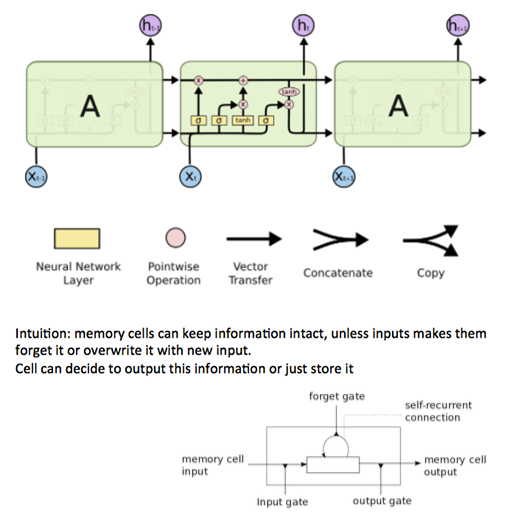
RNN按时间一层层展开,就是一层层深度,梯度会消失。梯度消失导致无法长期依赖,可使用门单元组件解决,如GRU、LSTM等。
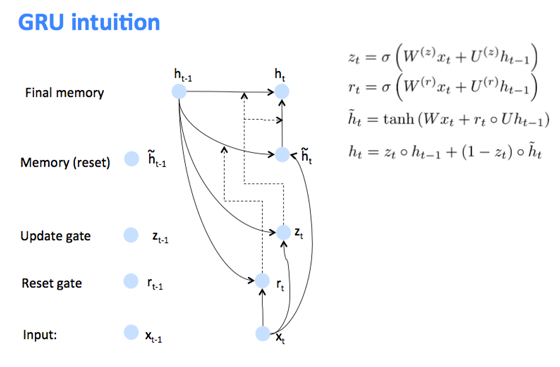
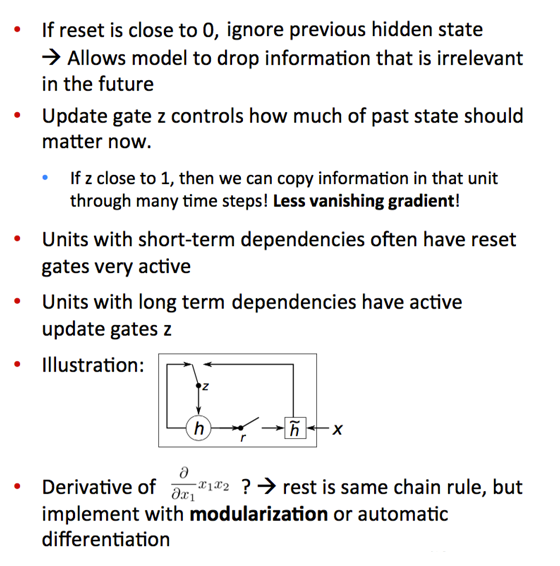
GRU(Gate Recurrent Unit,门控循环单元)
记忆细胞\(c^{<t>}=a^{<t>}\)记录t时刻的激活值, 按RNN激活值计算作为候选\(z^{<t>} = w_c [ c^{<t-1>}; x^{<t>} ] + b_c\),\(c’^{<t>}=tanh( z^{<t>} )\), 一个门(简化版)控制取候选\(c’^{<t>}\)还是取前一值\(c^{<t-1>}\),\(G_u=σ( 形似z^{<t>} )\),形似\(z^{<t>}\)有自己的w、b参数 \(c^{<t>} = G_u * c’^{<t>} + (1-G_u) * c^{<t-1>}\)。
因为\(G_{u}\)通常接近于0,\(c^{<t>}=c^{<t-1>}\),保持旧状态,没有梯度消失问题
LSTM(Long Short Term Memory,长短期记忆)
三个门,更新门\(G_u\)、忘记门\(G_f\)、输出门\(G_o\) \(z^{<t>} = w_c [ a^{<t-1>}; x^{<t>} ] + b_c\), \(c’^{<t>}=tanh( z^{<t>} )\), \(G_u = σ( 形似z^{<t>} )\), \(G_o = σ( 形似z^{<t>} )\), \(G_o = σ( 形似z^{<t>} )\),形似\(z^{<t>}\)有自己的w、b参数 \(c^{<t>} = G_u * c’^{<t>} + G_f * c^{<t-1>}\),\(a^{<t>} = G_o * c^{<t>}\)
词嵌入学习
用“词嵌入”表示单词,词嵌入向量表示单词与各种语义的关联度。
skip-grams:学习映射关系 context词=>附近某target词 负采样:选一个 context词=>附近某target词 作为正样本,再取一些到随机词的映射作为负样本,训练分辨映射是从附近词中选的还是随机选的 glove:统计target词在content词周围出现的次数,最小化它特定的代价函数
情感分类
词嵌入作输入,经过多对一RNN,再多元分类
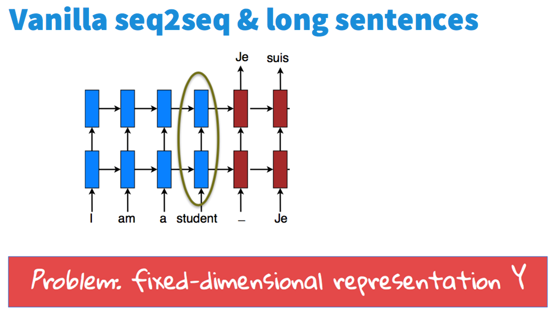
seq2seq模型(序列到序列)
一个encoder网络,接一个decoder网络
beam search(定向搜索)一次搜索k个最可能结果,是扩大搜索范围的贪婪搜索 要翻译句子,首先输入句子到encoder网络,decoder网络t=0时刻输出各单词概率,beam search选其中概率最高的k个进入t=1时刻。t=1时刻在试着选定第一个词的情况下算第二个词的概率,再选其中概率最高的k个。如此继续。
注意力模型
为解决先编码再解码的中间向量瓶颈,引入注意力模型。
在decoder的某时刻t,对encoder各时刻t’的输出值\(a^{<t’>}\)的注意力分布\(a^{<t,t’>}\),加权和\(\sum( a^{<t,t’>}a^{<t’>} )\)作为decoder时刻t的输入。
注意力分布\(a^{<t,t’>}\)由decoder时刻t-1的输出、encoder时刻t’的输出\(a^{<t'>}\)之间算相关度评分,再maxsoft归一化而得。相关度评分比如可以算两者的向量cos距离,或再引入个额外神经网络计算。
详细解释参见
语音识别
音频预处理成时频谱spectrogram:横坐标时间、纵坐标频率、颜色亮度表示能量强度。 > 频谱spectrum:时频谱中垂直于横坐标的截面,横坐标是频率、纵坐标是能量强度。
参考
- DeepLearning.ai by Andrew Ng
 词向量又称词嵌入(word embedding),把词映射到某几个特征构成的低维向量。embedding在数学上表示一个映射,该映射是单射的(每个Y只有唯一的X对应,反之亦然)、结构保存的(比如在X所属空间上X1<X2,那么映射后在Y所属空间上同样Y1<Y2)。
词向量又称词嵌入(word embedding),把词映射到某几个特征构成的低维向量。embedding在数学上表示一个映射,该映射是单射的(每个Y只有唯一的X对应,反之亦然)、结构保存的(比如在X所属空间上X1<X2,那么映射后在Y所属空间上同样Y1<Y2)。
 与邻近词
与邻近词




 Attention的想法是多记住一些源状态。
Attention的想法是多记住一些源状态。 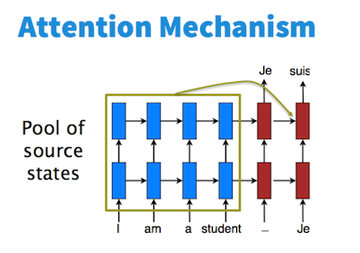 decoder算
decoder算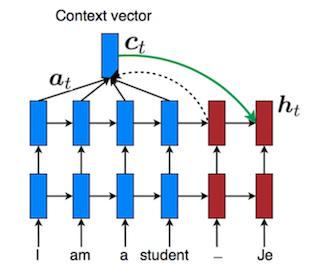
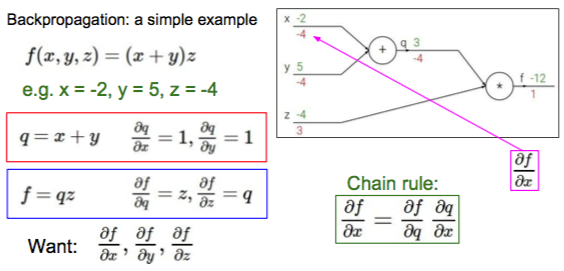
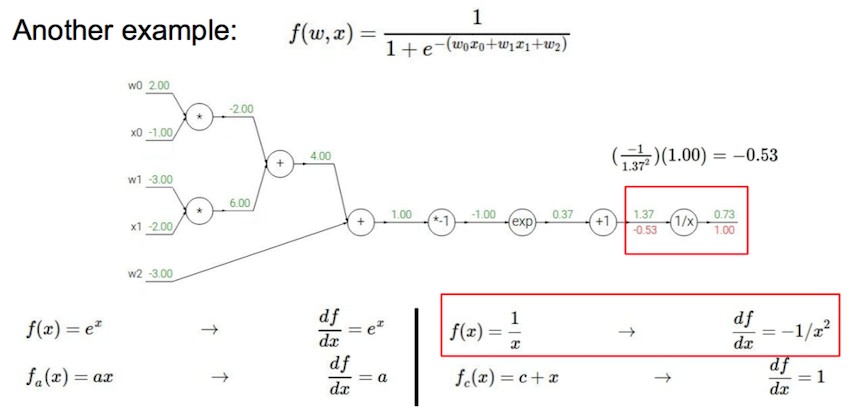 计算图节点可以按不同粒度组合
计算图节点可以按不同粒度组合 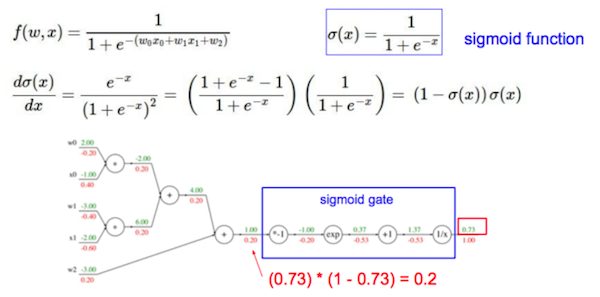
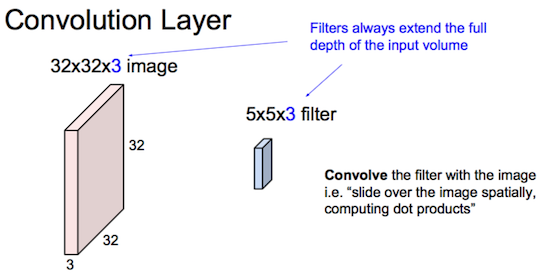
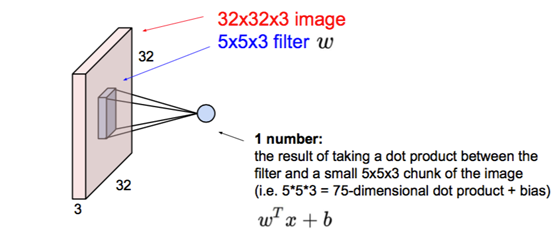
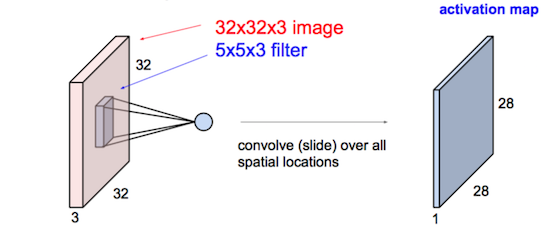
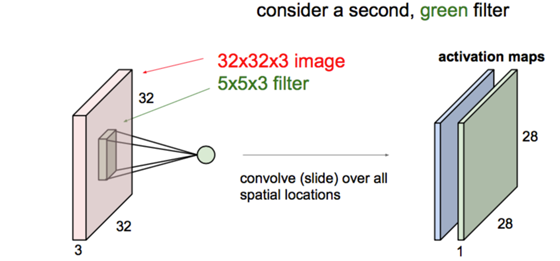
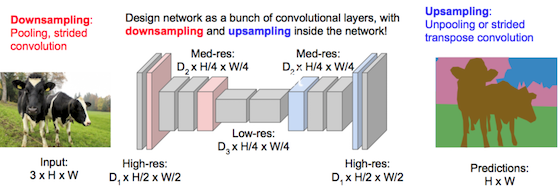
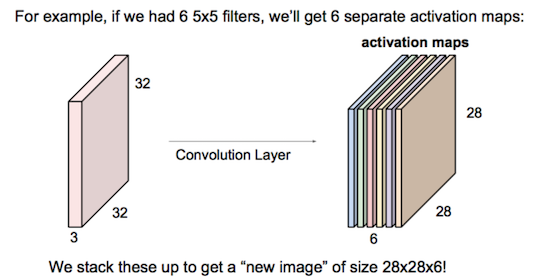 连续Conv+ReLU弄几层:
连续Conv+ReLU弄几层: 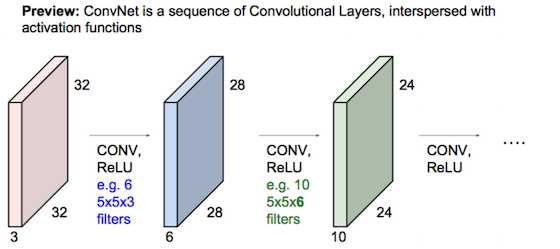 偶有Pool层降分辨率:
偶有Pool层降分辨率:  抽样方法比如:
抽样方法比如: 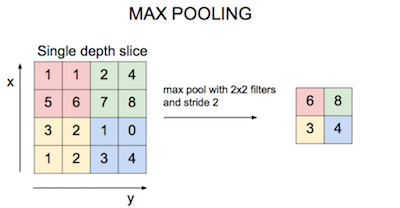 最后把输出展成一维向量,接入全连接层:
最后把输出展成一维向量,接入全连接层: 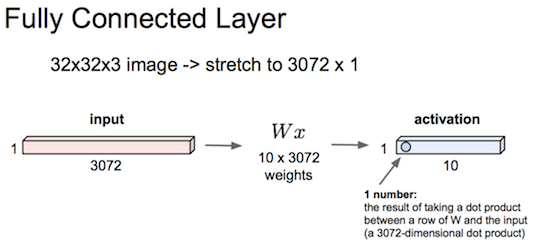


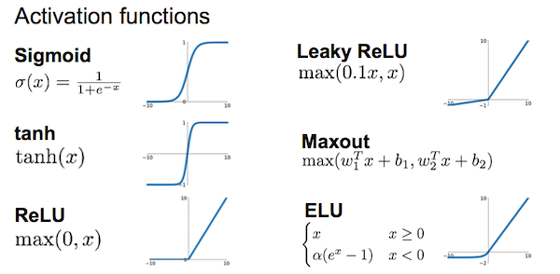
 sigmoid的导数在[0, 0.25],tanh的导数在[0, 1]
sigmoid的导数在[0, 0.25],tanh的导数在[0, 1] 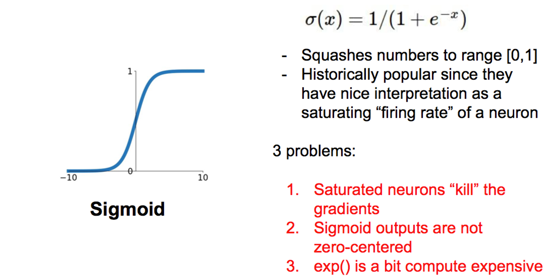
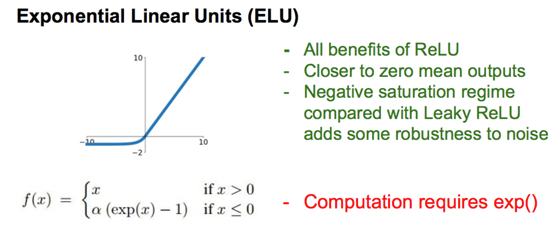
 ReLu当学习率大时梯度减得多,容易x<0变为dead。可减小学习率,或者使用Leaky ReLu、ELU。
ReLu当学习率大时梯度减得多,容易x<0变为dead。可减小学习率,或者使用Leaky ReLu、ELU。 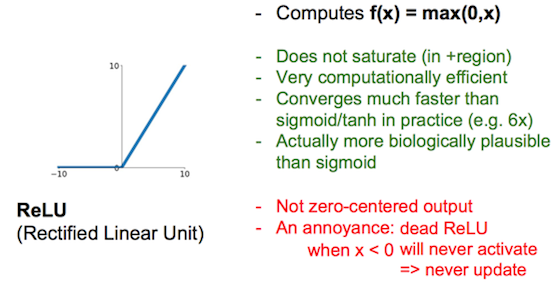




 更常用Adam优化 = Momentum + AdaGrad/RMSprop
更常用Adam优化 = Momentum + AdaGrad/RMSprop 

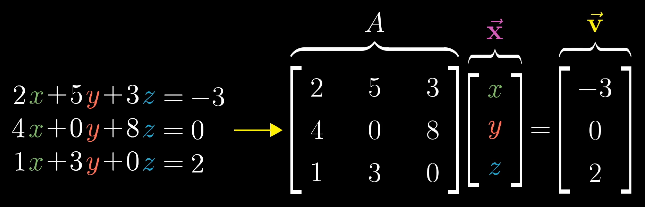
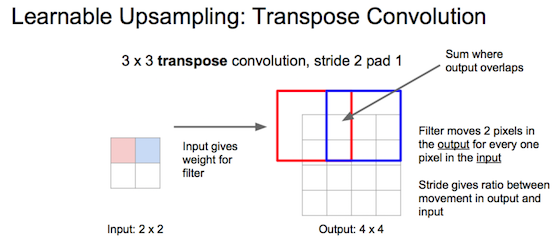 从矩阵乘法角度看
从矩阵乘法角度看 
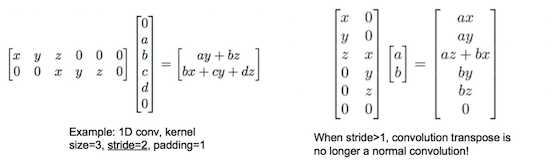




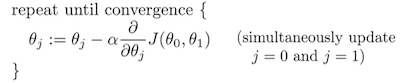 其中的α叫学习率,α太小下降太慢,α太大可能越过最低点来回振荡无法收敛。
其中的α叫学习率,α太小下降太慢,α太大可能越过最低点来回振荡无法收敛。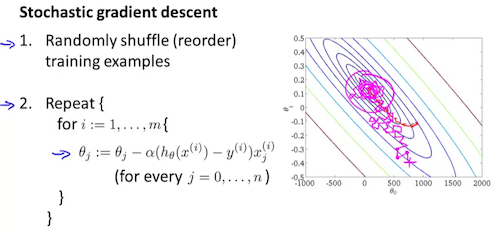
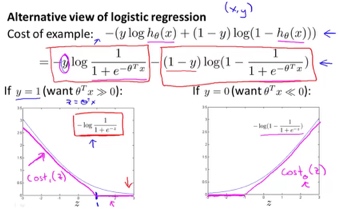
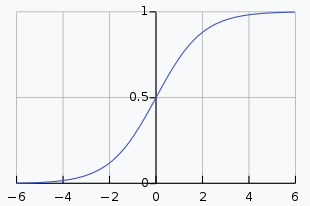 sigmoid性质:
sigmoid性质: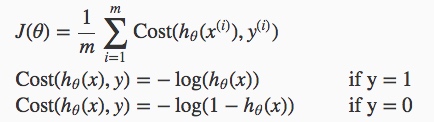 其中
其中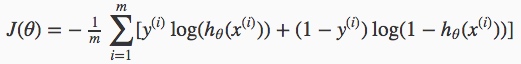 同样,需要得到使代价函数最小化的未知参数θ。可先算出一阶偏导数构成的梯度向量,然后用梯度下降法求解。
同样,需要得到使代价函数最小化的未知参数θ。可先算出一阶偏导数构成的梯度向量,然后用梯度下降法求解。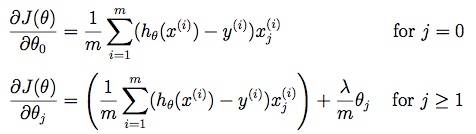 梯度下降法也相同
梯度下降法也相同 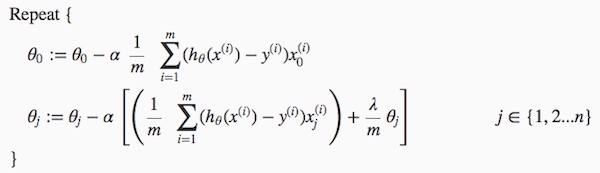 方程求解法正则化后变成
方程求解法正则化后变成 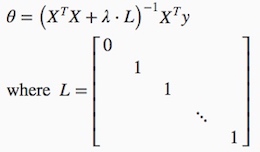

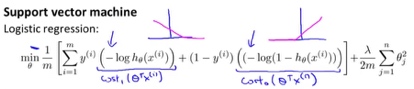 2. 要最小化J(θ),m倍数无所谓,A+λB变成CA+B形式(C=1/λ),就得到
2. 要最小化J(θ),m倍数无所谓,A+λB变成CA+B形式(C=1/λ),就得到 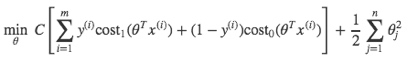
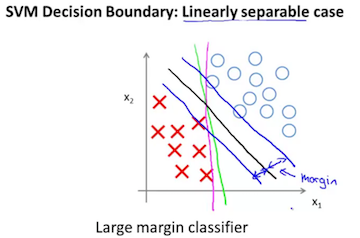 异常点存在时,小C值的间距大。
异常点存在时,小C值的间距大。 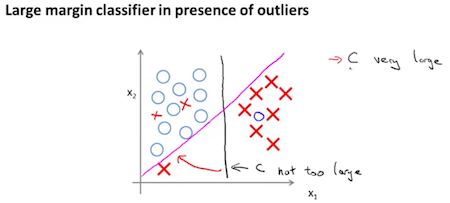
 如图中,通过3个landmark把2维特征x变成3维特征f,这里similarity函数就是kernel。 具体来说,这里用了高斯kernel:
如图中,通过3个landmark把2维特征x变成3维特征f,这里similarity函数就是kernel。 具体来说,这里用了高斯kernel: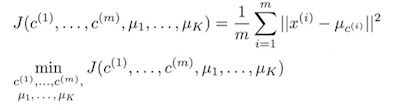 算法的两步正是固定μ优化c、固定c优化μ:
算法的两步正是固定μ优化c、固定c优化μ: 



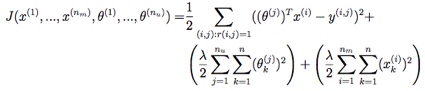 梯度,对x或θ的第k维特征求偏导。
梯度,对x或θ的第k维特征求偏导。