神经网络
后向传播其实就是使用导数的链式法则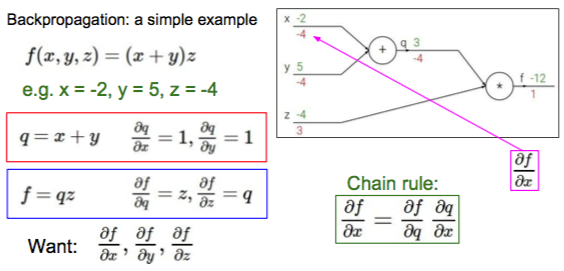 
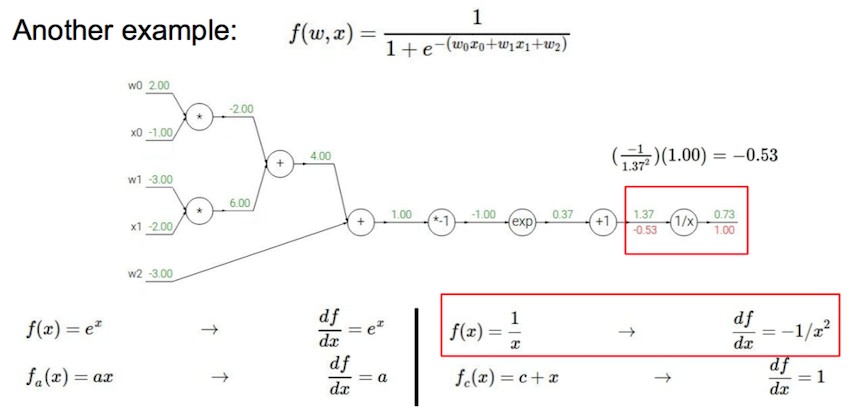计算图节点可以按不同粒度组合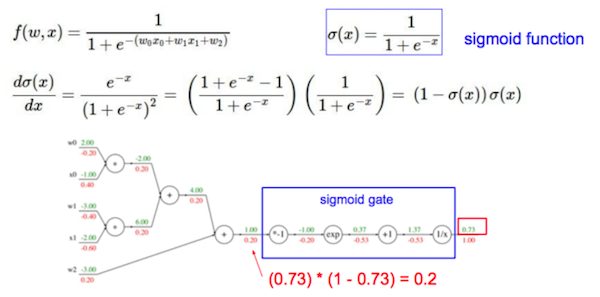 
卷积神经网络
过程：用filter卷积算得新图层，多个filters算得的图层叠成新图（卷积层），新图经ReLU处理；连续Conv+ReLU弄几层，偶有Pool层降分辨率；最后把输出展成一维向量，接入全连接层（神经网络）做多元分类。
卷积层：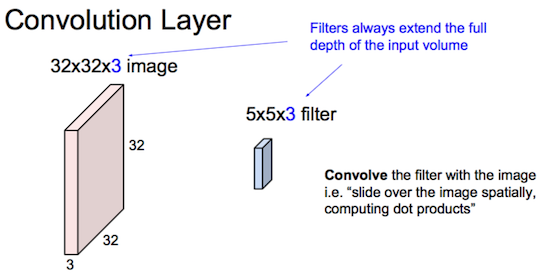 
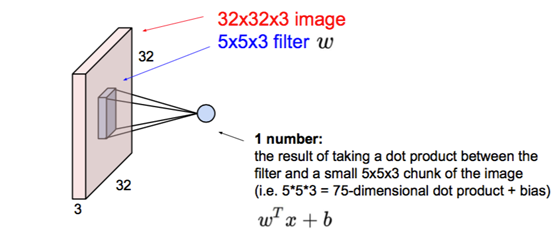
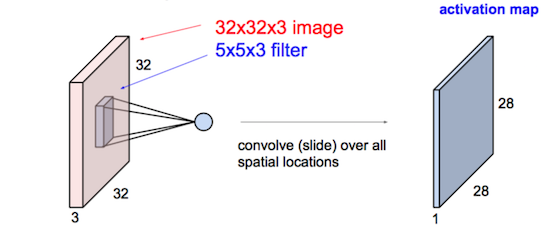
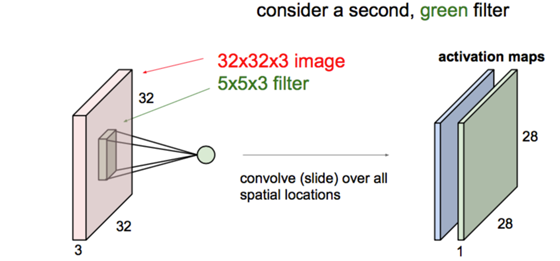
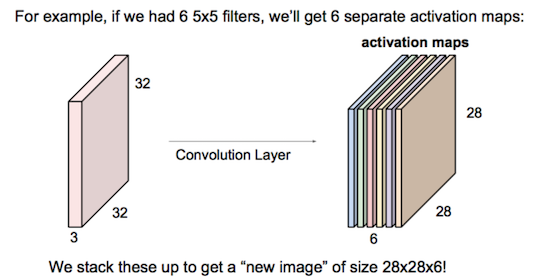连续Conv+ReLU弄几层： 
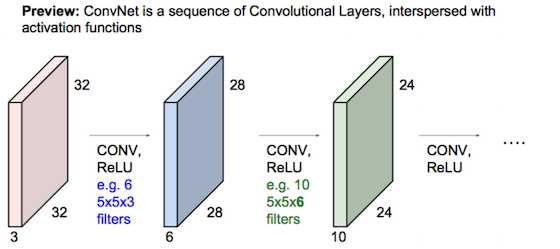偶有Pool层降分辨率： 
抽样方法比如： 
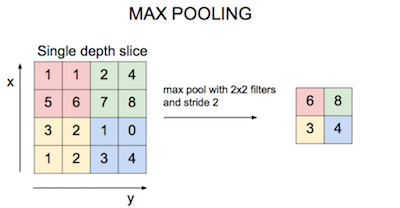最后把输出展成一维向量，接入全连接层：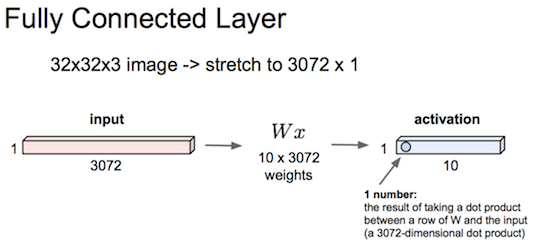 
典型的架构像这样： [(Conv-ReLU)*N-POOL?]*M-(FC-ReLU)*K-SoftMax
循环神经网络
各时刻共享权重参数W，由前一刻状态\(h_{t-1}\)、当前输入\(x_t\)计算新状态\(h_t\)、计算预测值\(y_t\)、计算\(loss_t\)；序列x全读完了总loss就是\(\sum loss_t\)，再后向传播计算梯度（backprop through time）、更新W。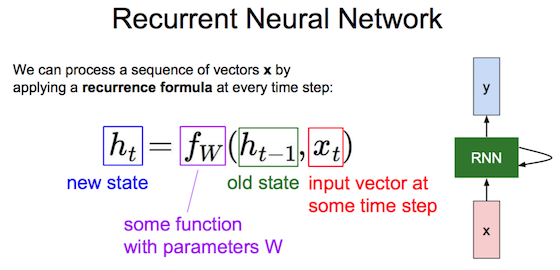 
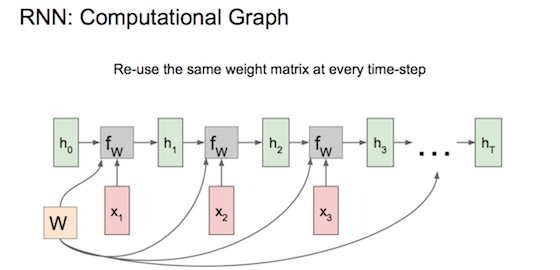
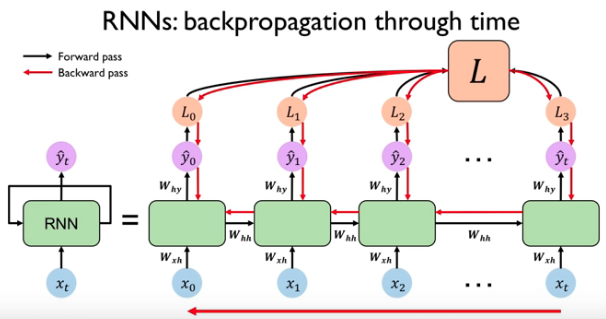
实践中，简单RNN难以描述长期依赖。更常用LSTM（Long Short Term Memory）、GRU（Gated Recurrent Unit），GRU比LSTM计算更少、效果相当。
多分类的loss函数
max margin
要让正确分类\(s_{y_i}\)比错误分类\(s_j\)的分数大（具体大多少无所谓，这里取大1）。满足这条件时loss为0、不满足时loss为\(s_j-s_{y_i}+1\)。 
softmax
常见激活函数
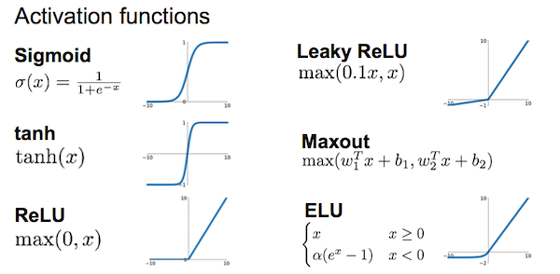
sigmoid的导数在[0, 0.25]，tanh的导数在[0, 1]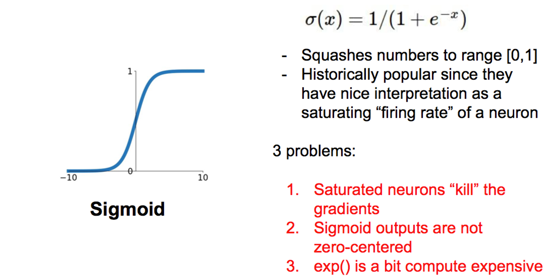 
ReLu当学习率大时梯度减得多，容易x<0变为dead。可减小学习率，或者使用Leaky ReLu、ELU。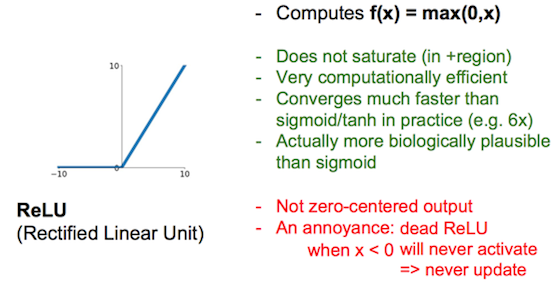 
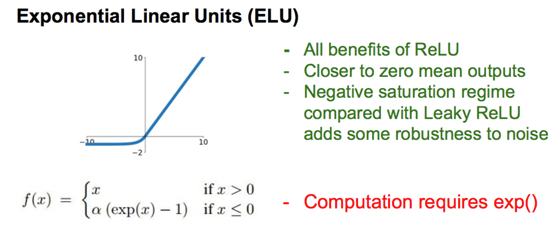
一些调优问题
train/validation/test
train集用于超参数选定后的模型训练，validation集用于验证超参数效果，test集只在最后出结果时用一次。交叉验证只在小数据集时有用。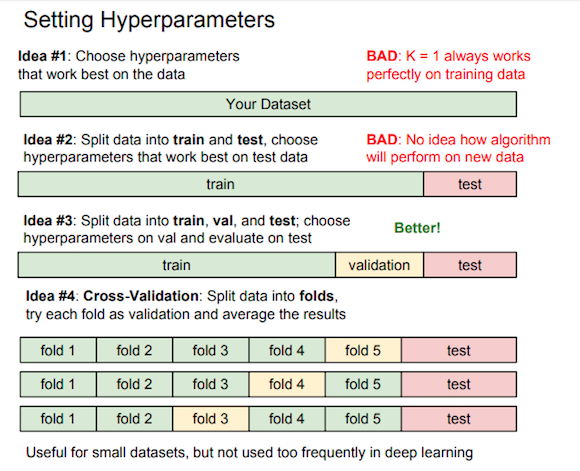 
初始化权重矩阵W
初始随机值太小或太大都不好。比如tanh作激活函数，若初始值太小，几次迭代后输出0。若初始值太大，函数饱和梯度=0。
可用Xavier初始法，W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in)。
若ReLU作激活函数，可用W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in/2)。
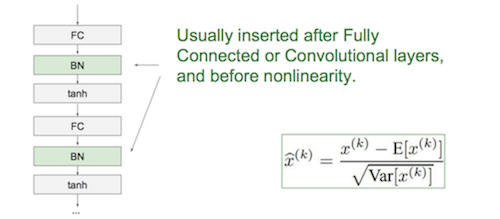
Batch Norm
训练时使用mini-batch的μ和σ修正数据：先让μ归0、σ归1，再加个BN层训练正态分布的缩放γ和平移β；测试时使用全部mini-batch上的移动平均μ和移动平均σ修正数据。 
随机梯度下降陷入局部极小值或鞍点
使用“Momentum”——移动平均梯度 
更常用Adam优化 = Momentum + AdaGrad/RMSprop 
dropout正则化
随机关闭每层一定比例的节点，强制丢掉一些信息防止过拟合。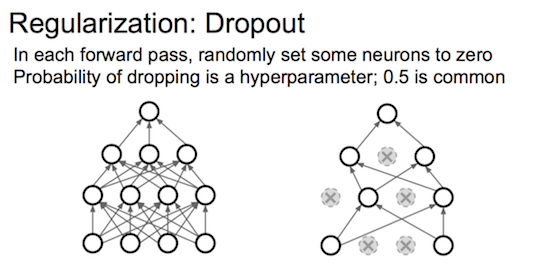 
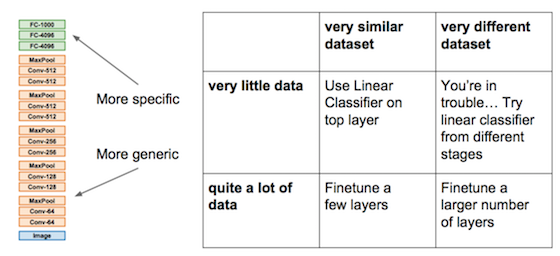
迁移学习
迁移到小数据集时，重训最后一层。迁移到较大数据集时，重训最后几层。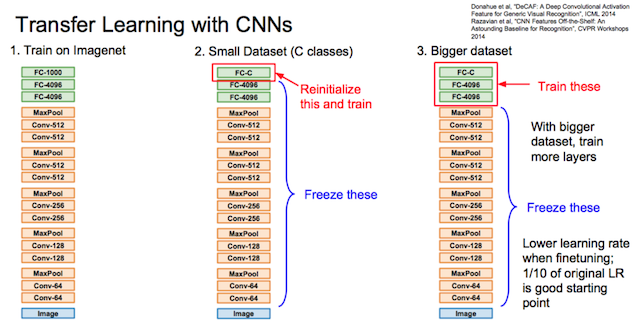 
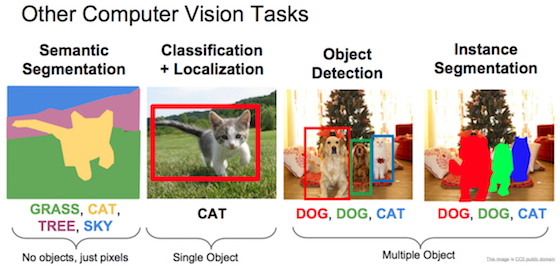
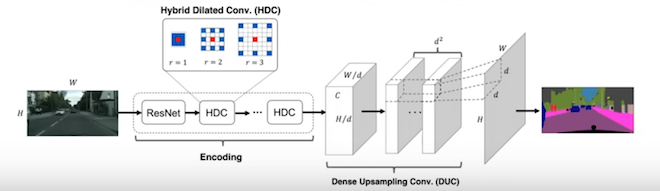
语义分割
全卷积层，先downsampling再upsampling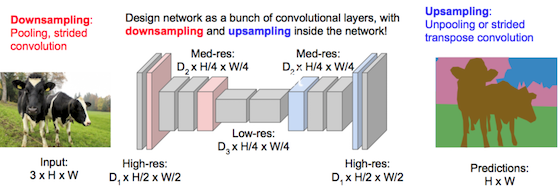 
转置卷积：一种upsampling方法
待upsampling的像素值、乘上filter、累加到输出的对应位置。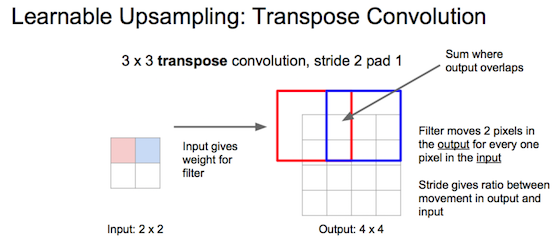 
从矩阵乘法角度看 
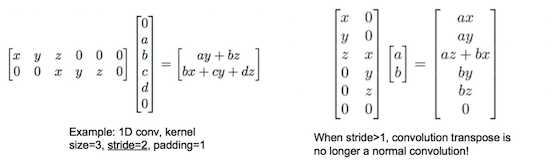
单个物体同时分类和定位
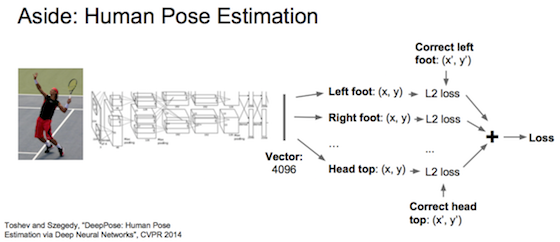
定位就是训练固定个数的定位参数，当作回归问题。如下面猫框有4个参数、姿势的关节位置有14个参数。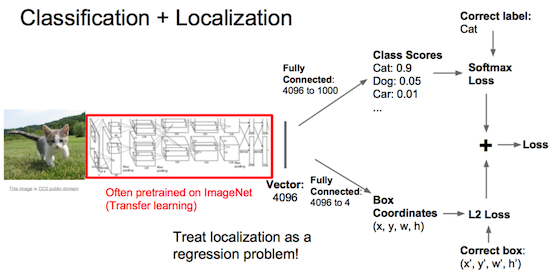 
多个物体的分类和定位
R-CNN（Region-based CNN）：要先用语义分割找出一些候选区域，再看这些区域是否包含关注列表中的物体并定位。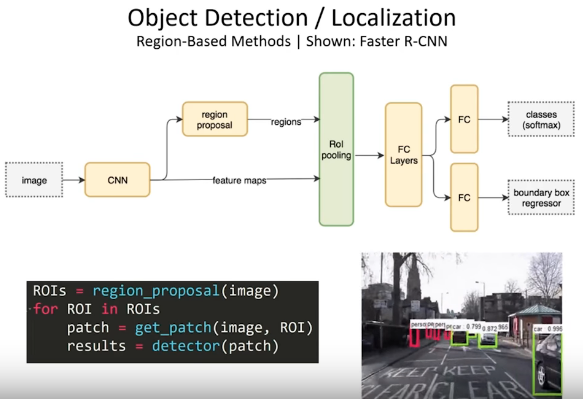 
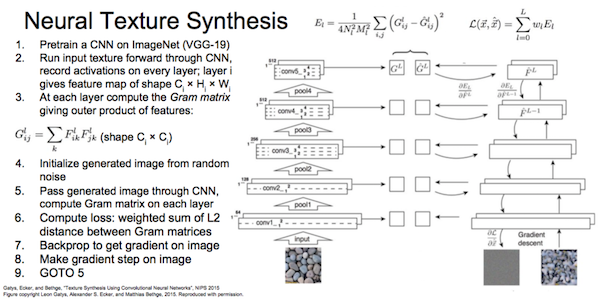
图片变成特定风格
内容相似：使生成图的各层激活情况尽量匹配原图。 风格相似：使生成图的各层gram矩阵尽量匹配原图各层。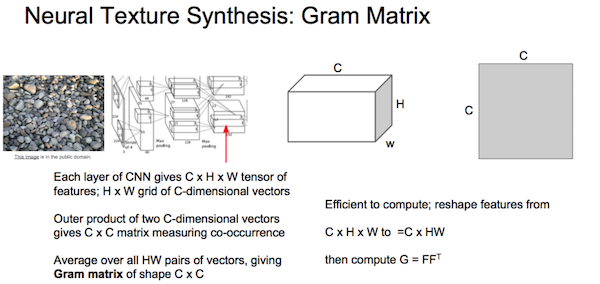 
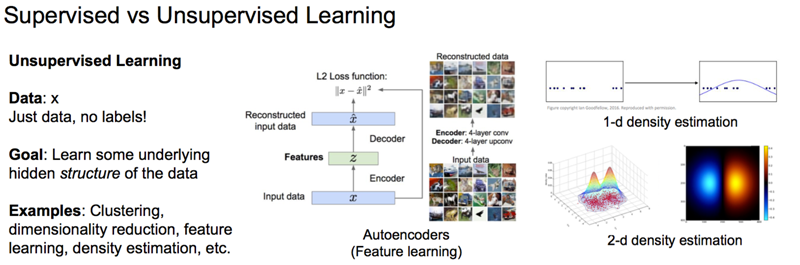
非监督学习
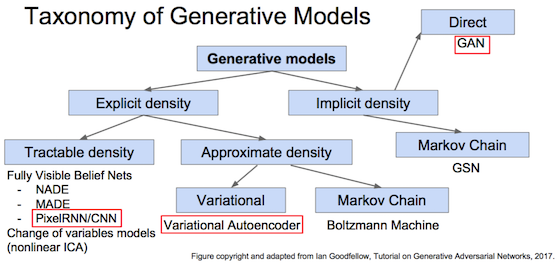
生成模型
生成符合训练集样本分布的新数据 
变分自编码器（Variational AutoEncoder）
参见Kevin Frans的解释，VAE就是给AutoEncoder里连接encoder和decoder中间的那个潜在变量添加限制，限制它符合单位正态分布。实现上训练出μ和σ，再从它们抽样出正态分布的潜在变量，就是下面的z。损失函数由两部分组成：潜在变量和单位正态分布的拟合度（KL散度），生成图像与输入图像的拟合度（均方误差）。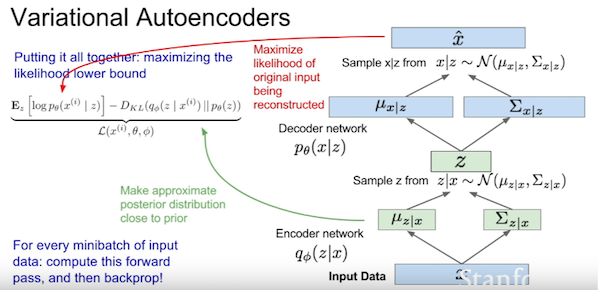 
生成对抗网络（Generative Adversarial Network）
对抗博弈，generator生成假图片，discriminator区分真假图片。 
强化学习
跟环境互动，最大化奖励。数学形式就是Markov决策过程。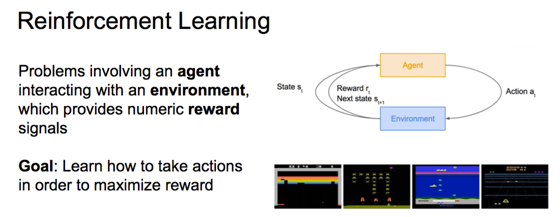 
Q-learning
使用神经网络拟合Q函数，因为Q-Learning表格维度巨大难以实用。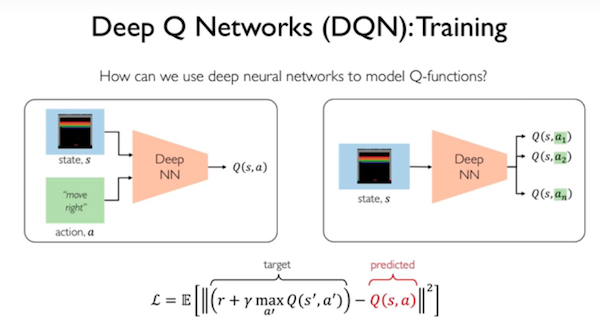 
Policy Gradient
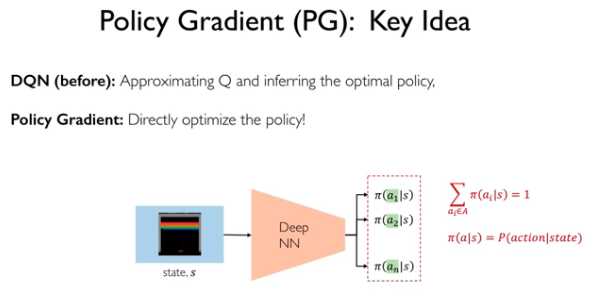
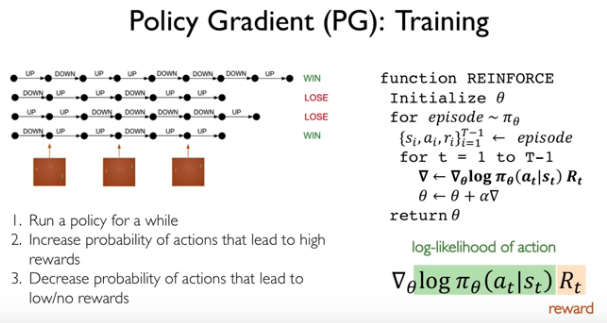
参考
- CS231n: Convolutional Neural Networks for Visual Recognition 2017
- Introduction to Deep Reinforcement Learning 6.S091, 6.S191, 2019