线性代数围绕两种基本运算:向量加法和向量数乘
向量:都指列向量。向量可看作是,把基向量i^, j^, …分别按照向量各数值缩放后的和
生成空间:一组向量线性组合后所能到达的点的集合
线性相关:如果某个向量落在其它向量的生成空间内,这个向量就与其它向量线性相关
线性变换:保持网格线平行且等距分布 的原点不变变换
左边乘矩阵M:跟线性变换等价,把基向量i^, j^, …分别变换成A的各列向量
行列式:线性变换的空间(二维面积或三维体积)缩放比例,负值表示空间被翻转(正向依右手定律)
行列式为0:线性变换将空间压缩到更小的维度上
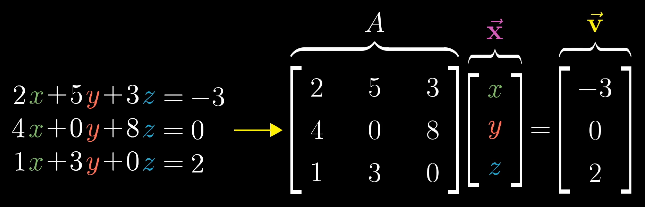
解线性方程组,就是要找未知向量x,x经过A变换后将变成v。要解线性方程组,需要看变换A是否将空间压缩到了更小的维度上,也就是看det(A)是否为0。如果det(A)≠0,不压缩空间,A的逆变换存在,\(x = A^{-1} * v\)。如果det(A)=0,压缩空间,逆变换不存在,x有解仅当v正好落在压缩后的空间内。比如说A将平面压缩为一条直线,x有解仅当v正好落在这直线上。
特别地,对于线性方程组Ax=0,x讲过A变换后变成零空间。若A不压缩空间,只能x=0。若x有非零解,只能A压缩空间,det(A)=0。
若变换A压缩空间,肯定有一个过原点的直线(降一维)或平面(降两维)被压缩到原点,这个被压缩的直线或平面就叫矩阵A的”零空间”或”核”,也是方程组Ax=0的解空间
秩:变换后(可能降维)的空间维数叫做变换的秩
满秩矩阵:变换后不降维
非方阵:mxn矩阵表示从n维空间到m维空间的变换
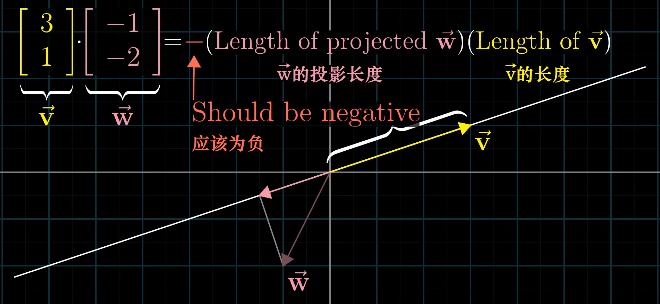
点积:两个向量的点积就是 一个向量在另一个向量上的投影长度 * 另一个向量的长度,方向不同时取负号
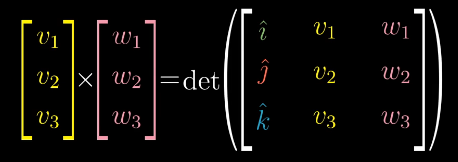
叉积:等价于 列向量矩阵的行列式(正向依右手定律)
基变换:其他基组在本坐标系下构成列向量矩阵P,P表示从其他基到本基的变换
相似矩阵:表达式 \(P^{-1} * A * P\) 代表同一变换的一种视角转换,中间矩阵A代表你所见的变换,外侧两矩阵代表视角的转换。\(P^{-1} * A * P\) 叫做相似矩阵,与A代表着同一个变换,只不过是从其他基的角度来看。总结就是,相似矩阵是同一变换的不同描述矩阵。
特征向量和特征值:线性变换后仍停留在原先直线上只被拉伸或压缩的向量叫做特征向量,拉伸或压缩的比例叫做特征值
特征基:若线性变换M有足够的特征向量,可从中选出能张成全空间的一些特征向量作为基,则在特征基视角下的相似矩阵 \(P^{-1} * A * P\) 为对角矩阵(因为特征基只被拉伸或压缩),这种“相似对角化”可以简化计算