监督学习
数据集已有正确答案,预测新数据的答案。预测连续值就是回归问题,预测离散值就是分类问题。
模型、代价函数
假设模型可以用h函数表示但参数未知,机器学习使用训练集为h训练参数,算出参数后的h就可以做些预测。 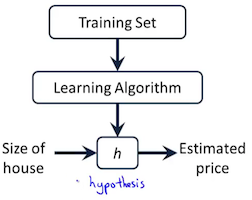
要训练得到怎样的参数?要得到使代价函数最小化的参数。 代价函数是关于这些未知参数的函数。比如线性回归的h函数是关于n维特征的多项式\(h_θ(x)=θ_0+θ_1x_1+θ_2x_2+...+θ_nx_n=θ^Tx\),可选平方误差作代价函数}$、 \(y^{(i)}\)指第i个样本的值。
梯度下降法
求最小化代价函数的参数,就是求函数取极值时的变量值。可用梯度下降法来迭代逼近局部最小值,当代价函数是凸函数时局部最小值就是全局最小值。所谓梯度,是指包含所有一阶偏导数的向量。
比如上面的线性回归问题,梯度下降法初始时先随便取组θ值,每次迭代就是各个维度都减去一点自己维上的梯度。相当于先在J(θ)的n+1维曲面上随便取个点,然后取周围使n+1维梯度下降最快的那个点,一步步迭代达到局部极小值。
比如2维的, 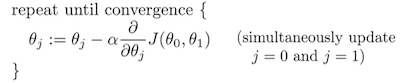 其中的α叫学习率,α太小下降太慢,α太大可能越过最低点来回振荡无法收敛。
其中的α叫学习率,α太小下降太慢,α太大可能越过最低点来回振荡无法收敛。
当有多个特征时,各特征的取值范围可能差别很大,在用梯度下降前要先把各特征值归一到较小区间,比如[-1,1]。方法比如将原先的\(x_i\)换成\(\frac{x_i-μ_i}{range(x)}\)或\(\frac{x_i-μ_i}{std(x)}\)。
梯度下降每次迭代要在所有m个样本上计算,速度太慢。实践中先把样本顺序打乱,然后每次在b个样本的minibatch上梯度下降,这就叫随机梯度下降。下图中b=1。 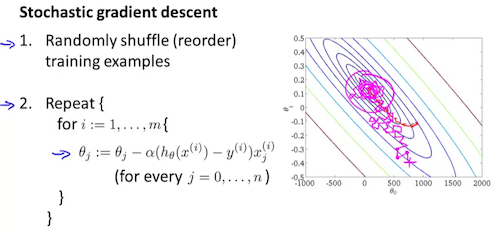
方程求解法
直接求解训练集m个样本构成的方程组。把m个样本的特征数据排成m*(n+1)的矩阵X(注\(x_0=1\)),m个样本的结果数据排成m*1的向量y,则\(Xθ=y, X^TXθ=X^Ty, θ=(X^TX)^{-1}X^Ty\)。之所以先\(X^TX\)可能为了先转成方阶再求逆。Octave代码pinv(X'*X)*X'*y,pinv是求伪逆。当然,向量化时也可把m个样本的特征数据排成(n+1)*m的矩阵,m个样本的结果数据排成1*m的向量y,然后\(θ^TX=y\),这样就跟单样本时\(θ^Tx=y\)形式相同。
方程法不需要选择学习率α,不需要将多特征的特征值归一到较小区间;缺点是求逆运算\(O(n^3)\),n不能太大。
二元分类
就是逻辑回归,用sigmoid函数将线性回归的值域变成(0,1),值>=0.5取y=1、值<0.5取y=0,这样就成了二元分类。
也就是说,逻辑回归模型的h函数是\(h_θ(x)=g(θ^Tx)\),其中\(g(z)=\frac{1}{1+e^{-z}}\)叫sigmoid函数或logistic函数,h(x)表示y=1的概率。对二元分类,由sigmoid曲线知,\(θ^Tx>=0\)取y=1,\(θ^Tx<0\)取y=0,\(θ^Tx\)就叫决策边界。 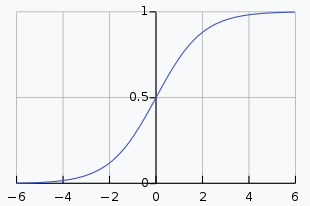 sigmoid性质:\(g'(z)=\frac{d}{dz}g(z)=g(z)(1-g(z))\)
sigmoid性质:\(g'(z)=\frac{d}{dz}g(z)=g(z)(1-g(z))\)
逻辑回归的代价函数定义如下,可以保证为凸函数: 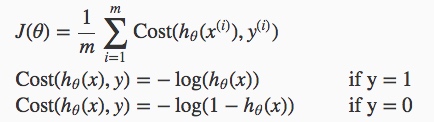 其中\(h_θ(x^{(i)})\)为样本预测值,\(y^{(i)}\)为样本实际值。合成一个,01分布的交叉熵:
其中\(h_θ(x^{(i)})\)为样本预测值,\(y^{(i)}\)为样本实际值。合成一个,01分布的交叉熵: 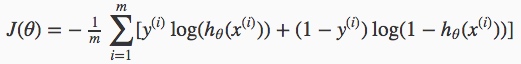 同样,需要得到使代价函数最小化的未知参数θ。可先算出一阶偏导数构成的梯度向量,然后用梯度下降法求解。
同样,需要得到使代价函数最小化的未知参数θ。可先算出一阶偏导数构成的梯度向量,然后用梯度下降法求解。
扩展到多元分类
为每个类训练一个“属于该类而不属于其他类”的“一对余”二元分类器,训练集的标签向量y要先转变成one-hot向量参与训练。要预测新数据属于哪一类,先计算新数据属于各个类的概率,取概率最大的那个类。
正则化
当特征太多时,模型容易太复杂、容易过拟合。为了防止过拟合,可以人工去掉一些不重要的特征,可以保留所有特征但减小特征参数\(θ_j\)(正则化)。
正则化范数惩罚\(θ_j\), j=[1..n]但不罚\(θ_0\)。在代价函数中加上\(\frac{λ}{2m}\sum_{j=1}^{n}θ_j^2\),λ越大则最终\(θ_j\)越小。λ叫正则化参数,这里除以2m是为了以后计算时方便。
线性回归和逻辑回归的梯度计算相同 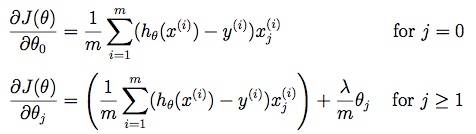 梯度下降法也相同
梯度下降法也相同 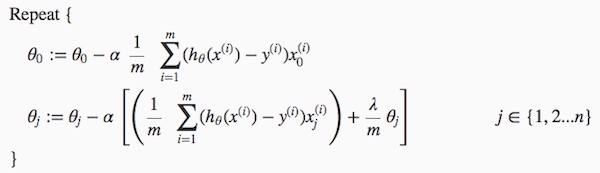 方程求解法正则化后变成
方程求解法正则化后变成 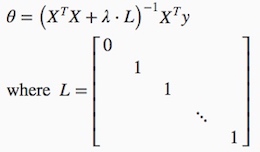
神经网络
处理非线性分类需要非线性的h函数,否则多项式h函数的特征数将指数级爆炸。
神经网络把逻辑单元(模拟神经元)按层组织。每个逻辑单元是个二元分类(逻辑回归),输入是一个总为1的偏置单元和上一层所有的逻辑单元。这样每层就是个多元分类,整个神经网络就是一层层的多元分类。
计算梯度的过程先前向传播计算各层输出、再反向传播计算各层梯度,反向一层层梯度计算其实就是“计算图”的导数链式计算。
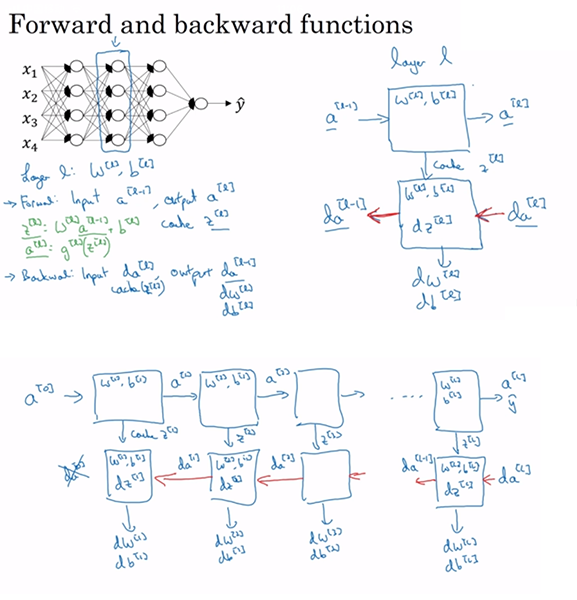
前向传播计算各层输出
\(a^{(l)}\)表示第l层输出(作为下一层输入时要记得添上那总为1的第一分量),\(Θ^{(l)}\)表示第l层到下一层的系数矩阵({下一层单元数}行 x {这一层单元数+1}列),设\(z^{(l)}=Θ^{(l)}a^{(l)}\),则\(a^{(l+1)}=g(z^{(l)})\)。
反向传播计算各层梯度
前向传播在知道一层到下一层的系数矩阵时计算下一层的值,但各层系数矩阵是未知的,需要我们通过最小化代价函数训练出来。神经网络的代价函数,是最终层逻辑单元的代价函数和(加上前面各层系数矩阵的正则化惩罚)。要最小化代价函数J(Θ),需求得各层梯度,即各层系数矩阵的偏导数\(D_{ij}^{(l)}=\frac{\partial}{\partialΘ_{ij}^{(l)}}J(Θ)\)。反向传播反向计算各层误差,最终算出各层梯度。这里引入记号,把J(Θ)关于\(z_j^{(l)}\)的偏导数\(δ_j^{(l)}\)叫做“误差”。
反向传播的过程:对每一个样本,先前向传播计算各层输出\(a^{(l)}\),再从最后一层往回倒,反向计算各层误差\(δ^{(l)}=(Θ^{(l)})^Tδ^{(l+1)} .* g’(z^{(l)}), g’(z^{(l)})=a^{(l)}.*(1-a^{(l)})\)并累加\(Δ^{(l)} = Δ^{(l)}+δ^{(l+1)}(a^{(l)})^T\),初始误差\(δ^{(L)}=a^{(L)}-y\)。处理完所有样本后,偏导数取平均值\(D_{ij}^{(l)}=\frac{1}{m}Δ_{ij}^{(l)}\) if j=0,\(D_{ij}^{(l)}=\frac{1}{m}Δ_{ij}^{(l)}+\frac{λ}{m}Θ_{ij}^{(l)}\) if j≥1。
注:初始化系数矩阵要用[-ε,ε]的随机小值。若用相同值将导致下层各逻辑单元毫无差别,若用大值将使sigmoid值接近1或0,斜率小梯度下降收敛慢。 后向传播计算结果可近似验证\(\frac{d}{dθ_i}J(θ) ≈ \frac{J(θ_1,…,θ_i+ε,…,θ_n)-J(θ_1,…,θ_i-ε,…,θ_n)}{2ε}\)。

关于激活函数
这里用sigmoid函数作例子,实际上可以为各层选择不同的激活函数。比如输出层还用sigmoid作二元分类;隐藏层可用tanh函数(相当于sigmoid平移缩放过原点),或更常见的ReLU函数g(z)=max{0,z}(Rectified Linear Unit,Geoffrey Hinton已证明ReLu几乎等同于一叠logistic单元)。 sigmoid函数:\(g(z)=\frac{1}{1+e^{-z}}, g'(z)=g(z)(1-g(z))\) tanh函数:\(g(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}, g'(z)=1-g^2(z)\) ReLU函数:\(g(z)=max(0,z), g'(z)=\begin{cases} 0& \text{if x<0}\\ 1& \text{if x≥0}\end{cases}\) leaky ReLU函数:\(g(z)=max(0.01z, z), g'(z)=\begin{cases} 0.01& \text{if x<0}\\ 1& \text{if x≥0}\end{cases}\)
支持向量机
非线性的h函数不知啥样不妨碍。只要知道代价函数J(θ)、算出梯度、训练出θ,就能预测 y=1 if \(θ^Tx≥0\)。
SVM的代价函数可从逻辑回归的代价函数推广得到: 1. 将代价函数从曲线变成分段线性的\(cost_1(z)\)和\(cost_0(z)\) 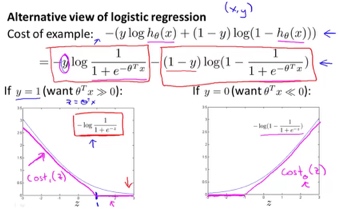
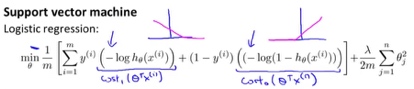 2. 要最小化J(θ),m倍数无所谓,A+λB变成CA+B形式(C=1/λ),就得到
2. 要最小化J(θ),m倍数无所谓,A+λB变成CA+B形式(C=1/λ),就得到 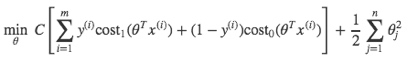
SVM是一种大间距二元分类器,最小化J(θ)造成决策边界在类间保持较大间距。 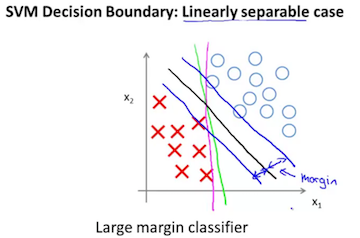 异常点存在时,小C值的间距大。
异常点存在时,小C值的间距大。 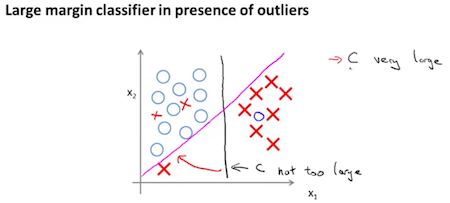
SVM是一种线性分类器,但实践中可以构造新特征并在新特征的维度上线性可分,这样就可应用于非线性问题。
核函数
把a维特征通过某种变换变成b维特征,这变换就叫kernel(核函数)。SVM通常用核函数把数据点映射到高维空间,低维空间上不好分,高维空间上容易分。  如图中,通过3个landmark把2维特征x变成3维特征f,这里similarity函数就是kernel。 具体来说,这里用了高斯kernel:\(f_i=similarity(x,l^{(i)})=exp(-\frac{||x-l^{(i)}||^2}{2σ^2})\)。当x接近\(l^{(i)}\),\(f_i≈1\);当x远离\(l^{(i)}\),\(f_i≈0\);带宽σ越大,x远离\(l^{(i)}\)时\(f_i\)越慢下降到0。
如图中,通过3个landmark把2维特征x变成3维特征f,这里similarity函数就是kernel。 具体来说,这里用了高斯kernel:\(f_i=similarity(x,l^{(i)})=exp(-\frac{||x-l^{(i)}||^2}{2σ^2})\)。当x接近\(l^{(i)}\),\(f_i≈1\);当x远离\(l^{(i)}\),\(f_i≈0\);带宽σ越大,x远离\(l^{(i)}\)时\(f_i\)越慢下降到0。
由于涉及多维特征,kernal变换前记得先特征值归一化。kernel变换后,最小化新特征f的代价函数来训练θ,对新数据x先转换成f表示后再预测 y=1 if \(θ^Tf>=0\)。
实践中若有m个样本x,就每个样本作一个landmark,得m个landmark。也就是说,把特征x变换成m维新特征f。
非监督学习
把无标签数据集分簇。
k-means
优化目标是最小化所有点与它们簇中心的距离平方和: 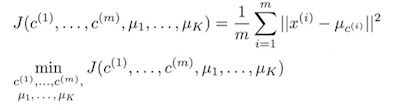 算法的两步正是固定μ优化c、固定c优化μ:
算法的两步正是固定μ优化c、固定c优化μ: 
簇数K通常是看数据分布后手动设置,初始化的K个簇中心是随机选的K个数据点。运行时如果某簇中心没有分配到数据点,这簇中心通常直接删掉,偶尔也可重新随机化。为防止k-means陷入局部最优解,要多次运行k-means取最小代价函数值。
特征降维:主成分分析
把n维点投射到k维面,最小化所有点与投射面的距离平方和\(\frac{1}{m}\sum_{i=1}^{m}||x^{(i)}-x_{approx}^{(i)}||^2\)。

在训练集计算协方差矩阵Sigma,将Sigma奇异值分解,取矩阵U的前k列。然后不管训练集验证集测试集,投射X到Z用\(Z=XU_k\),从Z倒推回X用\(X≈ZU_k^T\)。
怎么选择参数k? 
异常检测

选出有助于异常检测的n个特征,每一维特征用训练集算出\(μ_j\)和\(σ_j^2\),然后对新数据点累乘所有特征的正态分布概率,总概率太小就是异常点。 常识:正态分布有68%(稍大于2/3)的面积在μ±δ范围内。
为什么不用分类算法?因为训练数据中异常数据太少、异常类型太多,分类算法无法识别出异常特征。
怎么选出有助于异常检测的特征?用直方图\(hist(x_i)\)看特征\(x_i\)的分布,若不接近正态分布,可尝试变换特征使\(f(x_i)\)接近正态分布,\(f(xi)\)变换可以是\(log(x_i+c)\)、\(x_i^{\frac{1}{t}}\)等。也可对某异常创建特征,使异常点特征值远离均值(特别大或特别小)。
推荐系统
假设我们有一份用户对电影的部分评分表,在左边排列着电影名,在上边排列着用户名。对第j列第i行,\(r(i,j)\)表示用户j是否对电影i评过分,\(y^{(i,j)}\)表示用户j对电影i的评分。
有了这个评分表,我们能知道什么?
关键要理解两个隐藏变量:电影i的特征\(x_i\)(假设有n维)、用户j的偏好\(θ_j\)(维度同\(x_i\)一样)。如果知道这两个变量,用户j对电影i的评分就为\(θ_j^Tx_i\)。或者说,所有电影特征按行排列成矩阵X,所有用户偏好按行排列成矩阵Θ。如果知道这两个矩阵,用户对电影的评分矩阵就为\(XΘ^T\)。 如果这两个矩阵只知一个,结合评分表就能线性回归训练出另一个。我们把已知电影特征X求用户偏好Θ的过程,叫做基于内容的推荐。 如果这两个矩阵都不知道,可先随机赋值、再通过X→Θ→X→Θ→…的迭代求得收敛。实际上,我们能在一步迭代中同时收敛X和Θ,这种同时迭代X和Θ的过程叫做协同过滤。
协同过滤
代价函数对所有有评分的项(i,j)求和。 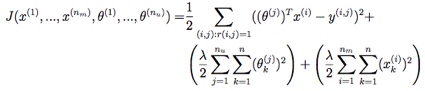 梯度,对x或θ的第k维特征求偏导。
梯度,对x或θ的第k维特征求偏导。 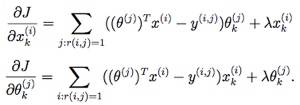

若新用户对所有电影都没评分,代价函数最小化会算得该用户偏好为零向量,这没什么用。可先在评分矩阵的每一行减去该行均值,再在新评分矩阵上训练X和Θ,最后算得的预测值再加回均值。 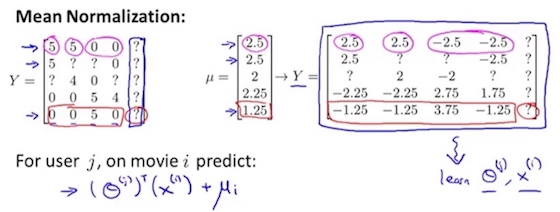
找相似的电影?\(||x_i-x_j||\)距离越小越相似。
参考
- Machine Learning Course by Andrew Ng, with exercises
- 理解交叉熵